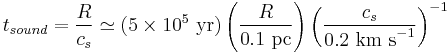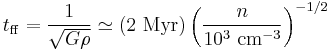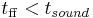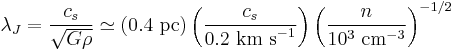Jeans instability

Star formation

Interstellar medium Molecular cloud Bok globule Dark nebula Young stellar object Protostar T Tauri star Herbig Ae/Be stars Nebular hypothesis
Object classes
Herbig–Haro object
Theoretical concepts
Initial mass function Jeans instability Kelvin–Helmholtz mechanism
Star portal

In physics, the Jeans instability causes the collapse of interstellar gas clouds and subsequent star formation. It occurs when the internal gas pressure is not strong enough to prevent gravitational collapse of a region filled with matter. For stability, the cloud must be in hydrostatic equilibrium, which in case of a spherical cloud translates to:

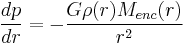$\frac{dp}{dr}=-\frac{G\rho(r) M_{enc}(r)}{r^2}$ ,

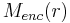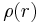where $M_{enc}(r)$ is the enclosed mass, $p$ is the pressure, $\rho(r)$ is the density of the gas at $r$ , $G$ is the gravitational constant and $r$ is the radius. The equilibrium is stable if small perturbations are damped and unstable if they are amplified. In general, the cloud is unstable if it is either very massive at a given temperature or very cool at a given mass for gravity to overcome the gas pressure.

Jeans mass

The Jeans mass is named after the British physicist Sir James Jeans, who considered the process of gravitational collapse within a gaseous cloud. He was able to show that, under appropriate conditions, a cloud, or part of one, would become unstable and begin to collapse when it lacked sufficient gaseous pressure support to balance the force of gravity. Remarkably, the cloud is stable for sufficiently small mass (at a given temperature and radius), but once this critical mass is exceeded, it will begin a process of runaway contraction until some other force can impede the collapse. He derived a formula for calculating this critical mass as a function of its density and temperature. The greater the mass of the cloud, the smaller its size, and the colder its temperature, the less stable it will be against gravitational collapse.

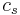The approximate value of the Jeans mass may be derived through a simple physical argument. One begins with a spherical gaseous region of radius $R$ , mass $M$ , and with a gaseous sound speed $c_s$ . Imagine that we compress the region slightly. It takes a time,

$t_{sound} = \frac{R}{c_s} \simeq (5 \times 10^5 \mbox{ yr}) \left(\frac{R}{0.1 \mbox{ pc}}\right) \left(\frac{c_s}{0.2 \mbox{ km s}^{-1}}\right)^{-1}$

for sound waves to cross the region, and attempt to push back and re-establish the system in pressure balance. At the same time, gravity will attempt to contract the system even further, and will do so on a free-fall time,

$t_{\rm ff} = \frac{1}{\sqrt{G \rho}} \simeq (2 \mbox{ Myr})\left(\frac{n}{10^3 \mbox{ cm}^{-3}}\right)^{-1/2}$

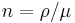where $G$ is the universal gravitational constant, $\rho$ is the gas density within the region, and $n = \rho/\mu$ is the gas number density for mean mass per particle 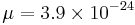$\mu = 3.9 \times 10^{-24}$ g, appropriate for molecular hydrogen with 20% helium by number. Now, when the sound-crossing time is less than the free-fall time, pressure forces win, and the system bounces back to a stable equilibrium. However, when the free-fall time is less than the sound-crossing time, gravity wins, and the region undergoes gravitational collapse. The condition for gravitational collapse is therefore:

$t_{\rm ff} < t_{sound}$

With a little bit of algebra, one can show that the resultant Jeans length 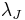$\lambda_J$ is approximately:

$\lambda_J = \frac{c_s}{\sqrt{G \rho}} \simeq (0.4 \mbox{ pc})\left(\frac{c_s}{0.2 \mbox{ km s}^{-1}}\right)\left(\frac{n}{10^3 \mbox{ cm}^{-3}}\right)^{-1/2}$

This length scale is known as the Jeans length. All scales larger than the Jeans length are unstable to gravitational collapse, whereas smaller scales are stable. The Jeans mass 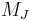$M_J$ is just the mass contained in a sphere of radius 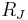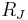$R_J$ ( $R_J$ is half the Jeans length):

$M_J = \left(\frac{4\pi}{3}\right) \rho R_J^3 = \left(\frac{\pi}{6}\right) \frac{c_s^3}{G^{3/2} \rho^{1/2}} \simeq (2 \mbox{ M}_{\odot}) \left(\frac{c_s}{0.2 \mbox{ km s}^{-1}}\right)^3 \left(\frac{n}{10^3 \mbox{ cm}^{-3}}\right)^{-1/2}$

It was later pointed out by other astrophysicists that in fact, the original analysis used by Jeans was flawed, for the following reason. In his formal analysis, Jeans assumed that the collapsing region of the cloud was surrounded by an infinite, static medium. In fact, because all scales greater than the Jeans length are also unstable to collapse, any initially static medium surrounding a collapsing region will in fact also be collapsing. As a result, the growth rate of the gravitational instability relative to the density of the collapsing background is slower than that predicted by Jeans' original analysis. This flaw has come to be known as the "Jeans swindle". Later analysis by Hunter corrects for this effect.

The Jeans instability likely determines when star formation occurs in molecular clouds.

Michael K.-H. Kiessling believes that Jeans' results can be vindicated without engaging in a mathematical swindle on the premise that "as long as we obtain a sensible dynamics in some sensible limit, we should not worry too much if some potential ceases to exist in the same limit" concluding that in his treatment "All the ad hoc steps of the 'Jeans swindle' have materialized in a mathematically clean way." Mathematical Vindications of the "Jeans Swindle"

References

Jeans, J. H. (1902). "The Stability of a Spherical Nebula". Philosophical Transactions of the Royal Society of London. Series A 199: 1–53. JSTOR 90845.
Longair, Malcolm S. (1998). Galaxy Formation. Berlin: Springer. ISBN 3540637850.
Clarke, Cathie; Carswell, Bob (2007). Astrophysical Fluid Dynamics. Cambridge: Cambridge University Press. ISBN 9780521853316.

Jeans instability

Jeans mass

See also

References